Research in
Machine Learning and Scientific Computing
I work at the intersection of machine learning, inverse problems, and the physical sciences. My research focuses on understanding how structure, algebraic, analytic, geometric, or physical, can be used to design algorithms that reason, rather than merely interpolate. I develop methods that combine data-driven learning with operator-level insights, aiming for models that are fast, stable, and scientifically interpretable.
I am especially interested in how learned local inverses, operators, and dynamical viewpoints can help solve challenging physical inference problems at scale. My long-term goal is to contribute foundational ideas that bridge mathematical analysis, computational methods, and scientific machine learning, and to help build a principled theory for next-generation intelligent systems in physics and beyond.
Selected Papers
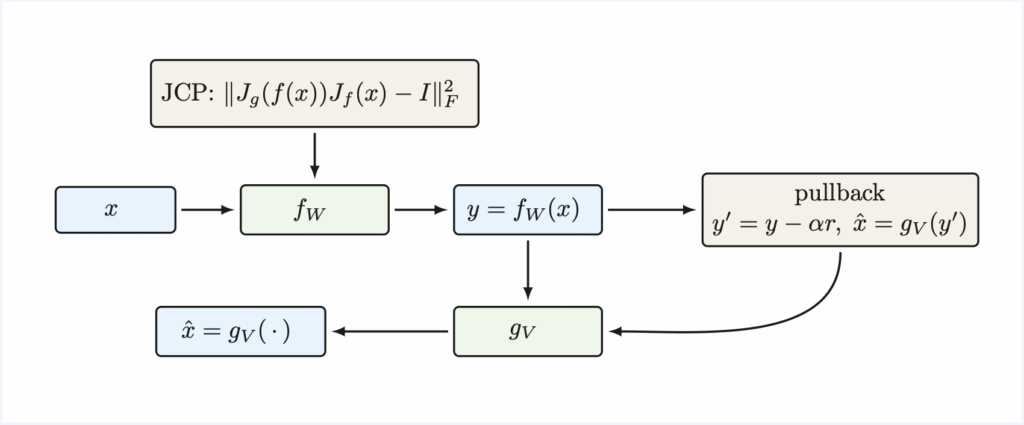
• Deceptron: Learned Local Inverses for Fast and Stable Physics Inversion
Aaditya L. Kachhadiya, NeurIPS ML4PS 2025
Theoretical Machine Learning and Optimization
Coming soon